文档类参考

文档类选项

字体选项（建议使用 fandol）：

• adobe：使用 adobe 字体
• ubuntu：使用 ubuntu 字体
• windows：使用 windows 字体
• fandol：使用 fandol 字体，随 texlive 默认安装
• mac：使用 mac 字体

版式选项：

• standard：A4 标准版。每个题目有一定空隙（大概3cm左右），每道题目的内容会强制在同一页，对于选择题而言，题目和选项不会跨业出现；
• loose：A4宽松版。每页会有 2 题，对于较长的题目，会自动占用一页；
• compact：A4紧凑版。题目间无任何空隙；
• single：A4单题版。一页只会出现一题；
• padl：横版Pad版。平板刷题，一页一题，适合小题（选择题和填空题）；
• padp：竖版Pad版。平板刷题，一页一题，适合大题。

其他选项：

• printmode：只在A4版下有效，可生成适合双面打印的文档
• water：是否显示全局页面水印（水印图片可在配置文件中自定义，水印将显示在页面右下角）
• online：在封面显示在线文档链接

封面设置

打开 config.tex，以下配置项可自定义封面内容：

% 封面设置
\CoverImg{img/cov01.jpg} % 封面图片
\PreTitle{ExBook · 刷题本模板} % 前置标题
\Title{此处填写主标题} % 主标题
\TitleDescription{此处填写副标题} % 副标题
\TypeOne{A4紧凑版} % A4紧凑版下的类型标识
\TypeTwo{A4标准版} % A4标准版下的类型标识
\TypeThree{横版Pad版} % 横版Pad版下的类型标识
\TypeFour{A4宽松版} % A4宽松版下的类型标识
\TypeFive{A4单题版} % A4单题版下的类型标识
\TypeSix{竖版Pad版} % 竖版Pad版下的类型标识
\motto{你这个年龄是怎么睡得着觉的} % 封面座右铭
\Creator{研小布} % 制作人
\UpdateTime{\today} % 更新时间
\OnlineCheckUrl{https://github.com/ExBook/ExBook} % 在线勘误文档地址

说明如下：

页眉页脚设置

打开 config.tex，以下配置项可自定义页眉页脚：

% 页眉页脚设置
\Lhead{微信公众号·研小布} % 左页眉 
\Chead{2025考研} % 中页眉、平板模式（padl或padp）下页眉中间的文字
\Rhead{408WD数据结构选择题刷题本} % 右页眉、平板模式（padl或padp）下页眉右侧的文字
\LheadC{公众号·研小布·} % 平板模式（padl或padp）下页眉左侧的文字

主题颜色设置

打开 config.tex，以下配置项可自定义颜色主题（默认为\blue）：

% 页眉页脚设置
\setThemeColor{\blue}

ExBook 提供4种经典颜色和8种个性颜色。

• 4种经典颜色主题

  

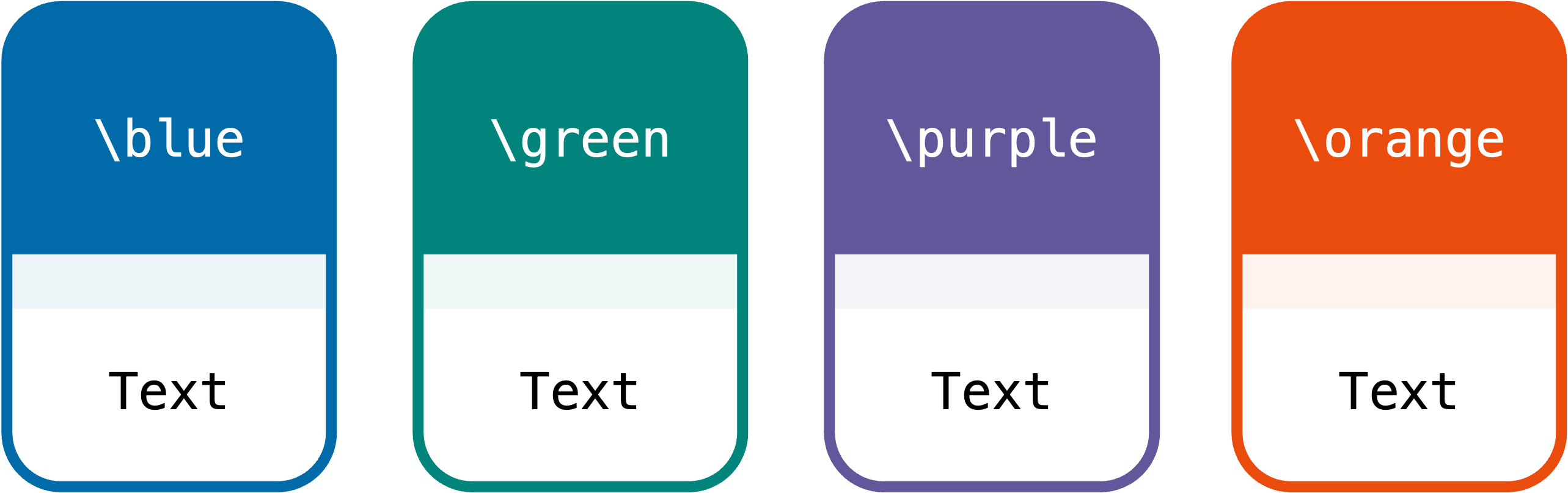
  如果你是一个专门制作做题本/刷题本的博主，那么建议选择这四种经典颜色。

• 8种个性颜色主题

  

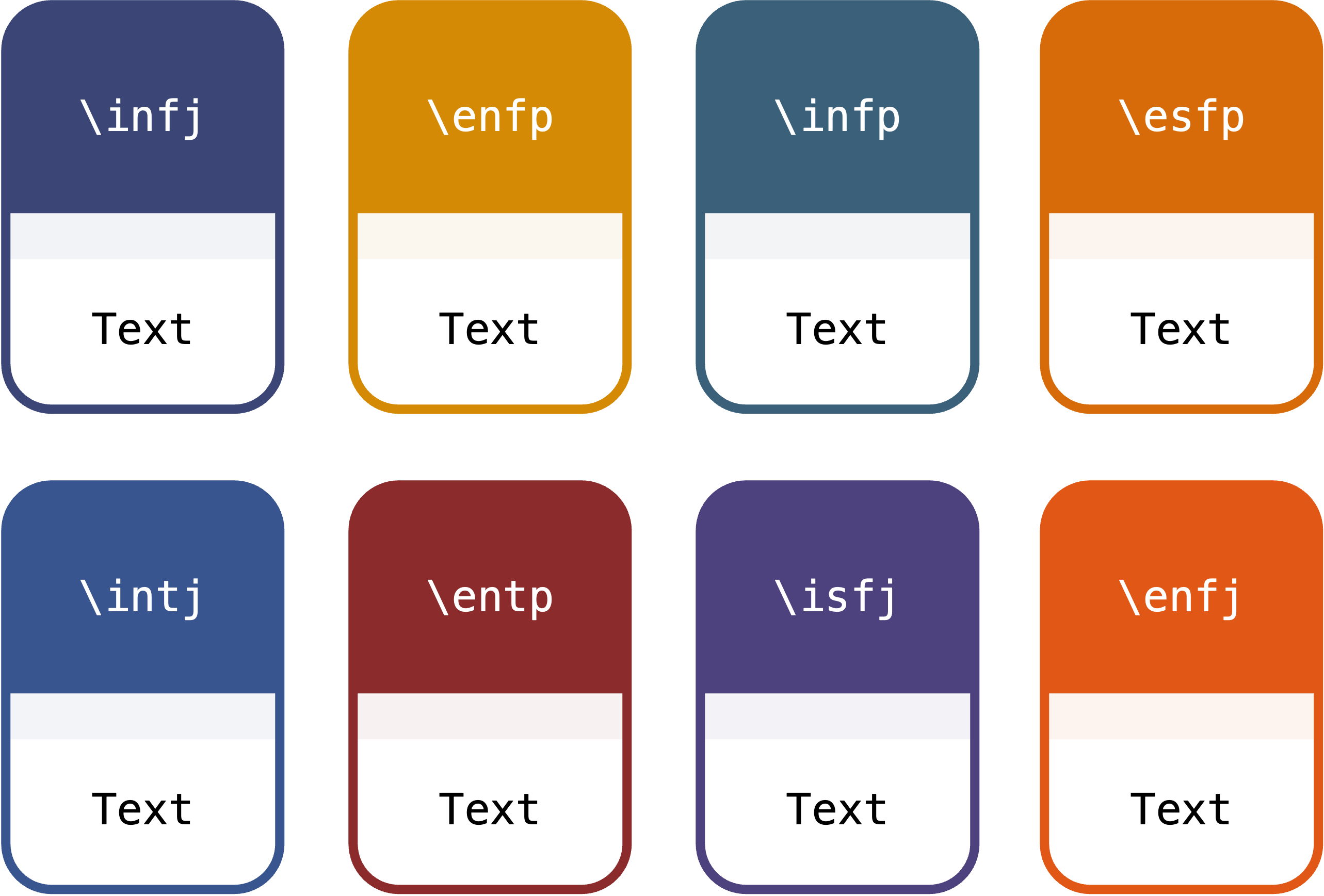
  这八种个性颜色分别来自八种常见的MBTI人格的代表色，可以选择你自己喜欢的颜色。

题目录入环境及命令

1. 题组环境

   \begin{qitems}[r]
   
   \end{qitems}
   

   环境选项：r（从 1 开始计数）

2. 题目环境

   \begin{bbox}
   
   \end{bbox}
   

3. 题目命令

   \qitem 题目内容
   

4. 小问环境

    \begin{subqitems}
            \subqitem 第一小问
            \subqitem 第二小问
    \end{subqitems}
   

5. 选择题选项命令

    \threechoices{选项内容}{选项内容}{选项内容}         % 四个选项
    \fourchoices{选项内容}{选项内容}{选项内容}{选项内容}        % 五个选项
    \fivechoices{选项内容}{选项内容}{选项内容}{选项内容}{选项内容}      % 六个选项
    \sixchoices{选项内容}{选项内容}{选项内容}{选项内容}{选项内容}{选项内容}{选项内容}   % 七个选项
   

6. 代码高亮环境

   \begin{lstlisting}[escapeinside={(*@}{@*)}]
    此处输入代码
   \end{lstlisting}
   

7. 其他命令

   • 空括号（英文和中文）

     \blankbox % 中文空括号
     \eblankbox % 英文空括号
     

   • 空下划线

     \blankline % 空下划线
     

   • 文字水印命令

     \textwater % 文字水印的内容在 config.tex 中自定义
     

   • 插入题目图片命令

     \imgin{0.2}{fig/img01.png} % 第一个参数为缩放比例，第二个参数为图片路径
     

   • 答案页指示命令

     \qanswerloc{10} % 将会显示 “此部分答案见原书 P10”
     

页面水印设置

打开 config.tex，以下配置项可自定义全局页面水印：

\WaterImg{img/water.png} % 图片水印 出现在页面的右下角

完整例子

• main.tex

  % 使用 ExBook 文档类，并传递选项
  \documentclass[cs4size,fandol,standard,online]{ExBook} 
  
  \begin{document}
  
  \include{config} % 示例文件
  \maketitle 
  
  % 免责声明文件
  \include{contents/pre} % 示例文件
  
  \setcounter{page}{1}
  \tableofcontents
  
  \clearpage 
  
  \include{contents/content_type_one} % 示例文件
  % \include{contents/content_type_two} % 示例文件
  
  \end{document}
  

• content_type_one.tex

  \section{自定义章节标题一}
  \subsection{第一章第1节}\qanswerloc{10}
  
  \begin{qitems}[r]
  
      \begin{bbox}
          \qitem   设$f(x)$满足$2f(x)+f(1-x)=x^2$，则$f(x)=\blankline.$
      \end{bbox}
  
      \begin{bbox}
          \qitem   设$f(x)=2x+\sqrt{x^{2}+2x+1}$，$g(x)=
          \begin{cases}
          x+2, & x\geqslant0, \\
          x-1, & x<0,  
          \end{cases}$，则$g[f(x)]= \blankline$.
      \end{bbox}
  
      \begin{bbox}
          \qitem   设某项目用于 发和宣传 总成本为$a$万元 当 发和宣传所 成本分别为$x$万元和 $y$ 万元时， 收益为$R=2x^{\frac{1}{3}}y^{\frac{1}{2}}$万元,则收 最大时，研发所用成本为\blankline.
      \end{bbox}
  
      \begin{bbox}
          \qitem   已知 $\lim\limits_{x\to0}\dfrac{f(x)}{x}$ 存在，且函数
          $$f(x)=\ln(1+x)+2x\bullet\lim_{x\to0}\frac{f(x)}{\sin x}$$
          则$\lim\limits_{x\to0}\dfrac{f(x)}{x}=$ \blankline.
      \end{bbox}
  
      \begin{bbox}
          \qitem  可以用\blankbox 定义一个完整的数据结构。\textwater
  
          \fourchoices{数据元素}{数据对象}{数据关系}{抽象数据类型}     
      \end{bbox}
  
      \begin{bbox}
          \qitem   若某算法的空间复杂度为$O(1)$，则表示该算法\blankbox 。
          \fourchoices
          {不需要任何辅助空间}
          {所需辅助空间大小与问题规模$n$无关}
          {不需要任何空间}
          {所需空间大小与问题规模$n$无关}
      \end{bbox}
  \end{qitems}
  
  \subsection{第一章第2节}
  \qanswerloc{15}
  
  \begin{qitems}[tr]
  
      \begin{bbox}
          \qitem   下列关于时间复杂度的函数中，时间复杂度最小的是\blankbox 。
          \fourchoices
          {$T_1(n)=n\log_2n +5000n$}
          {$T_2(n)=n^2 - 800n$}
          {$T_3(n)=n\log_2n - 6000n$}
          {$T_4(n)=20000\log_2n$}
      \end{bbox}
  
      \begin{bbox}
          \qitem   【2017 统考真题】 下列函数的时间复杂度是 \blankbox 。
          \begin{lstlisting}
      int func(int n){
          int i=0, sum=0;
          while(sum<n) sum += ++i;
          return i;
      }
          \end{lstlisting}
          \fourchoices{$O(\log n)$}{$O(n^{\frac{1}{2}})$}{$O(n)$}{$O(n\log n)$}
      \end{bbox}
  
  \end{qitems}
  
  \section{自定义章节标题二}
  \subsection{第二章第1节}
  \qanswerloc{20}
  \begin{qitems}[tr]
  
      \begin{bbox}
          \qitem  已知曲线$L:y=\ln\sqrt{x}(2\leqslant x\leqslant4)$，在$L$ 上的任意点$P(x,y)$作切线，记切线与曲线$L$在 $2\leqslant x\leqslant4$
          时所围成的有界区域的面积为$S$.
          \begin{subqitems}
              \subqitem 求一点$P_0$，使上述面积$S$关于$x$的变化率为零；
              \subqitem 当点$P(x,y)$在曲线上移动至$(\mathrm{e},\dfrac{1}{2})$时，横坐标关于时间的变化率为1，求此时面积关于时间的变化率$\dfrac{\mathrm{d}S}{\mathrm{d}t}.$
          \end{subqitems}
  
      \end{bbox}
  
      \begin{bbox}
          \qitem 以 $yOz$ 面上的平面曲线段$y=f(z)(z\geqslant0)$ 绕$z$轴旋转一周所成旋转曲面与xOy 面围成一个无上盖容器(见图)，现以 3 cm$^3/$s 的速率把水注人容器内，水面的面积以$\pi$ c$m^2$/ s 的速率增大.已知容器底面积为 16$\pi$ c$m^2$,求曲线$y=f(z)$的方程.
          \imgin{0.2}{fig/img01.png}
  
          % \includegraphics[width=0.2\textwidth]{img/img01.png}
      \end{bbox}
  
      \begin{bbox}
          \qitem   分析以下各程序段， 求出算法的时间复杂度.
          \begin{lstlisting}[escapeinside={(*@}{@*)}]
      (*@\ding{172}:@*)
      i=1; k=0;
      while(i<n-1){
          k=k+10*i;
          i++;
      }
  
      (*@\ding{173}:@*)
      y=0;
      while((y+1)*(y+1)<=n)
      y=y+1;
  
      (*@\ding{174}:@*)
      for(i=0;i<n;i++)
          for(j=0;j<m;j++)
              a[i][j]=0;
  
  
          \end{lstlisting}
      \end{bbox}
  
      \begin{bbox}
          \qitem   【2011 统考真题】一个长度为 $L$（$L\geqslant 1$ ）的升序序列$ S$, 处在第$\lceil L/2\rceil $个位置的数称为 $S$
          的中位数。例如，若序列 $S_1$=（11,13,15,17,19）, 则 $S_1$的中位数是 15, 两 个序列的中位
          数是含它们所有元素的升序序列的中位数。例如，若 $S_2$ =（2,4,6,8,20）, 则$S_1$和$S_2$的中
          位数是 11。现在有两 个等长升序序列$A$和$B$, 试设计一个在时间和空间两 方面都尽可能
          高效的算法，找出两个序列 $A$和$B$的中位数。要求：
          \begin{subqitems}
              \subqitem 给出算法的基本设计思想
              \subqitem  根据设计思想，采用 C 或 C++或 Java 语言描述算法，关键之处给出注释
              \subqitem 说明你所设计算法的时间复杂度和空间复杂度
          \end{subqitems}
      \end{bbox}
  \end{qitems}
  

显示效果见文档 main.pdf